• How To Plot Xbar And R-bar Chart In Excel Template

Interpreting an X-bar / R ChartAlways look at the Range chart first. The control limits on the are derived from the average range, so if the Range chart is out of control, then the control limits on the X-bar chart are meaningless.Interpreting the Range ChartOn the Range chart, look for out of control points and violations. If there are any, then the must be eliminated. And conduct to find those process elements that contribute to sporadic changes in variation. Remove the statistical bias of the out of control points by dropping them from the calculations of the average Range, Range control limits, average X-bar and X-bar control limits.

Click SigmaXL Control Charts X-Bar & R. Check Use Entire Data Table. Select Shots 1-3, click Numeric Data Variables (Y). Ensure that Calculate Limits is selected. The resulting X-bar & R charts are displayed: The control limits here were calculated including subgroups 21 to 25 which have a known assignable cause. We’ll learn a Control Chart from the Control Chart Excel template. The important point about Control Chart is how to use. Xbar-R Control Chart: Let’s make it with Excel and Spanish Template【Excel Template】. When plot(s) are beyond the upper or lower control limit line. We’ve already learned this. You can plot the graph by groups with the fill= cyl mapping. R takes care automatically of the colors based on the levels of cyl variable; Output: Step 5) Change the size To make the graph looks prettier, you reduce the width of the bar.

(This can be done automatically using the Auto Drop feature in our ).Also on the range chart, there should be more than five distinct values plotted, and no one value should appear more than 25% of the time. If there are values repeated too often, then you have inadequate resolution of your measurements, which will adversely affect your control limit calculations. In this case, look at how you measure the variable, and try to measure it more precisely.Once the effect of the out of control points have been removed from the Range chart, look at the X-bar Chart.Interpreting the X-bar ChartAfter reviewing the Range chart, interpret the points on the X-bar chart relative to the control limits.

Never consider the points on the X-bar chart relative to, since the observations from the process vary much more than the subgroup averages.If there are any out of control points on the X-bar Chart, then the must be eliminated. And conduct to find those process elements that contribute to sporadic changes in process location. Remove the statistical bias of the out of control points by dropping them from the calculations of the average X-bar and X-bar control limits. (This can be done automatically using the Auto Drop feature in our ).If the process shows control relative to the statistical limits and Run Tests for a, then we can analyze relative to requirements. Process capability is only meaningful when the process is stable, since we cannot predict the outcome of an unstable process.See also:Learn more about the SPC principles and toolsfor process improvement in (2011, McGraw-Hill) by,in his (only $39), or his( $350) or( $499). Since 1982: The art & science to improve your bottom lineQuality Americaoffers Statistical Process Control software, as well as training materials for Lean SixSigma, Quality Management and SPC.

We embrace a customer-driven approach, and lead inmany software innovations, continually seeking ways to provide our customers with thebest and most affordable solutions. Leaders in their field, Quality America has providedsoftware and training products and services to tens of thousands of companies in over25 countries.Menu.

Xbar and R ChartIf so, you most likely used some type of software package to display your data and compute the necessary control limits for your Xbar and R chart. But, have you ever wondered how these control limits for an Xbar and R chart were computed?For those of you that had to perform the calculations by hand, chances are you applied Xbar and R chart formulas using various control chart constants.

I know I did! I recall looking up values for A 2 and D 4 without any idea where they came from.The truth is; computing control limits isn’t that complicated. And, while the control chart constants used to compute control limits appears to be a mystery, they are quite easy to understand and derive.In this article, I’ll show you how to derive the following constants: d 2, d 3, A 2, D 3, and D 4. I’ll also show you how to use them to compute control limits for the Xbar and R chart. And it’s not that complicated.

Knowing where these constants come from and how you can derive them through simple simulations will improve your knowledge and deepen your appreciation of statistical process control. After you go through this article, you’ll be building Xbar and R charts with easy and confidence! It all starts with this chart The Range ChartTo build control limits for a Range chart we need to estimate the standard deviation, σ. We can estimate σ from m subgroups taken from a process. Each subgroup is a collection of n samples made under like conditions.

To assure we collect n samples made under like conditions, we collect consecutive samples over a short period of time. Doing so assures the conditions that produced the first sample are likely the same for the remaining n-1 samples.

As such, the data that describes a feature derived from n like samples estimates common cause variation.For each subgroup we compute the range and plot those values on the Range chart. The Range is the smallest value subtracted from the largest value in a subgroup. To estimate the standard deviation (σ) we compute the average Range across m subgroups and divide by a correction factor, called d 2.

In this article, I’ll focus on the range method and illustrate how we can derive the constants: d 2, d 3, D 3 and D 4 used to compute the control limits for a Range chart. Let’s talk about the basics 1.0 Computing the RangeLet’s say that x 1, x 2, x n describes a single value, of a part feature, from n samples. To compute the range, we take the difference between the largest and smallest value as shown in the expression below.R = x max – x min This next part is critical! 2.0 Computing d 2 and d 3 using the Relative Range, WIn statistics, there is a relationship between the range of a sample, from a normal distribution, and the standard deviation of that distribution. We can describe that relationship as a random variable W = R / σ.

We call this variable (W) the Relative Range. The parameters of the distribution of W (mean and standard deviation) are a function of the sample size n. The mean and standard deviation of W is d 2 and d 3. As such, an estimator of the standard deviation is s = R/d 2.

In Table 1, shown are the values of d 2 for the samples sizes n = 2, 3, 4, 5, 6, and 7. Xbar and R Chart ConstantsShown in Figure 1 is a simulation of 10 million distributed range values for n=5. I used normally distributed values having a mean and standard deviation of 0 and 1 to compute the range. The mean of the distribution of range values is d 2 and the standard deviation is d 3.

In this case, d 2 = 2.326 and d 3 = 0.864.Refer to the following post,. It explains, in further detail, how to estimate the d 2 constant and use it to compute the standard deviation.Let’s put what we learned into practice! 3.0 Computing the Average Range, and standard deviation, s.If R 1, R 2,R M represent the range for each sample, then we can find the average range using the following expression.To compute the average range, we sum the ranges (R i) and divide by the number of subgroups (m).Now that we have the average range ( ) we can estimate the standard deviation, σ. To do so, we will estimate the standard deviation by rearranging the Relative Range. Since W = R/σ, then σ = R/W. We can estimate σ using the standard deviation, s.

We can estimate the Range (R) using the average Range ( ) and the value of W which is the mean of the distribution of ranges (d 2).How accurate is the Average Range ( )? 4.0 The Relative Efficiency of the Range to estimate the variance, s 2.For small samples sizes between n = 2 through n = 6, the range method provides a good estimate of the sample variance s 2. In table 2, I show the relative efficiency of the range method to estimate the variance, s 2.

Beyond n = 6 samples per subgroup, the relative efficiency deteriorates. This is especially true after n = 10 samples per subgroup. But, for small samples sizes, say n = 2 to n = 5 the relative efficiency is good and satisfactory.

Xbar and R Chart Constants Let’s derive and compute the control limits! 5.0 Computing control limits about the subgroup averagesIf we use as an estimator of μ and as an estimator of σ, then the parameters of the chart are:We call UCL and LCL upper and lower control limits.

To compute the control limits for the chart we use as an estimate of the process center (or mean) μ. Here is the average of the m subgroup averages. For a process operating in control we expect that each new subgroup, m+1, will have an average that falls within.

6.0 The A 2 ConstantAs mention earlier, is the average across all m subgroup averages and represents the process centre. To simplify the control limit expressions (UCL, LCL) we make the following substitution:The A 2 constant only depends on the subgroup same size n.

Using A 2 we can rewrite the control limit expressions as follows.The constant A 2 is tabulated for various sample sizes in Table 3. Xbar and R Chart Constants 7.0 Computing the Upper and Lower Control Limits for the Ranges – Deriving D 3 & D 4So far, we have shown that the subgroup range relates to the process standard deviation. It is thus possible to observe process variability by plotting the subgroup Range values. For this reason we call this type of plot a Range Chart. The parameters of the Range Chart are easily found. The average Range, is the centreline.

How To Plot Xbar And R-bar Chart In Excel Template

To determine the upper and lower control limits about, we need an estimator of the standard deviation of the Ranges. Recall that we found the standard deviation of the distribution of range values for n=5 in figure 1. Note that we can find the standard deviation of the Ranges from the distribution of the Relative Range (W = R/σ). The standard deviation of W, called d 3, is a known function of n.

Let’s rearrange the Relative Range, W, and express it as a function of the Range, R. R = WσThe standard deviation of the range is:Since σ is unknown, we may estimate using:Now that we have an estimate of the standard deviation of the Ranges we can compute the 3-sigma control limits using these expressions.We can simplify these expressions by making the following substitution.andSubstituting D 3 and D 4 into the control limit expression we have,In Table 4, the constants D 3 and D 4 are shown for subgroup sample sizes n. Xbar and R Chart ConstantsWhen we use few subgroups to construct a X-bar and Range chart, we often consider these as trial control limits. In such a case, we still plot the subgroup averages and ranges on the control chart. The series of subgroup average and range values should display a random pattern. That is, there should not be evidence to suggest special cause variation. We observe special cause variation if any value falls beyond the control limits or when a consecutive values form a trend.

When we notice such special cause events, we should investigate. If these special cause events have an assignable cause, we should remove those values and use new trial control limits.

Here’s the best part! An Xbar and R Chart Case Study! 8.0 Xbar and R Chart Case StudyA metal stamping press makes metal parts used in automotive seating. A manufacturing Engineer wishes to establish statistical control of a critical feature; hole diameter. The Engineer collects twenty-five subgroups (m=25). Each subgroup contains n=5 consecutive samples collected each hour.

The data appears in Table 4. Using this data, we will compute the control limits and display an Xbar and R chart. Table 5: Xbar and R Chart Case Study Data The Range (R) ChartWhen working with an Xbar and R chart, we begin with the R chart. The control limits for the chart depends on the process variability,.

If the Range chart is not in control, the control limits for the chart will have no meaning. Once we compute the control limits for the Range chart, we will study the range chart for control. Using the data from Table 4, we will compute the center line for the R chart.For n=5 sample per subgroup, we find that D 3 = 0 and D 4 = 2.115.

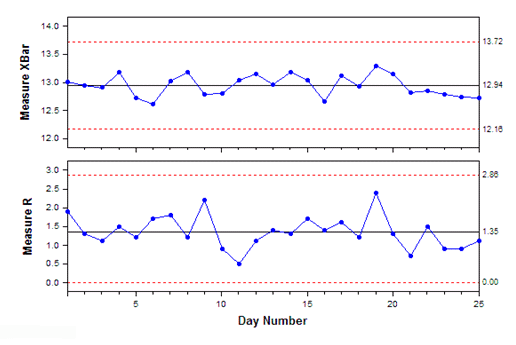
Therefore, the control limits for the R chart are:The 25 sample range values along with the centerline and upper control limit appear in the Range chart shown in Figure 2. The Range chart does not reveal any out-of-control condition. As such, the range chart suggests the process variability is stable and in control. Based on this observation we will use to compute the control limits for the chart.

Figure 2: Range ChartTo build the chart, we will use the data from Table 4.Computing the Control Limits for the Xbar ChartTo compute the control limits for the chart we will use A 2 = 0.577 from Table 3 for a subgroup sample size of n=5.Shown in Figure 3 is the chart. When we plot the 25 sample subgroup averages on this chart, the plot does not reveal any out-of-control conditions. We therefore conclude the Xbar and Range charts exhibit control. Going forward, we will adopt these trial control limits for use in online statistical process control. Figure 3: Xbar Chart Now!This article provides a foundation readers can use to derive and build their own Xbar and R chart.

I showed how we can derive the Xbar and R chart constants, d 2 and d 3,through simulation and used those constants to compute control limits for the Xbar and Range chart.In our example, we computed trial control limits that we will use to check a process with time. From time to time, the Xbar and R chart will not exhibit control.

When the Xbar and R chart does not exhibit control we will need to identify special cause events. Finding special cause events is a critical practice. It demands that we determine when such an event started, how long it lasted, and what type of special cause variation is at work. Knowing the type of variation, when it started, and how long it lasted helps isolate a potential root cause. Identifying a potential root cause drives continuous improvement.

This, we will discuss in a follow-up article.For additional information, on the Xbar and R Chart, please refer to the following. If you are interested is seeing how you can visualize and estimate the d2 and d3 constants then watch the video below! Download movavi photo editor cracked. X Bar: 320 310 330 360 290 280 340 320 360 300R: 12 16 14 18 22 23 10 13 27 25A packaging machine packs tea in plastic packets.

To ensure consistent quantity in each packet a sample of 30 packets were taken per hour in a day and its mean and range is recorded. Around 10 such sample were taken per day. From the following data answer the following questions.Q.No 1: Comment on the type of data being collected, which control chart is appropriate for the data and why.Q.No 2: what are the values for Central Line, Upper control limit and lower control limit, also show the entire calculations for the response.Q.No 3: What are your interpretations for the above samples, can we accept that the system is in control,give justification for you answer.Can you please solve this with explanation. Hello Ajay.I am amazed at how many times I get this same question!So, lets deal with question 1. Which control chart is appropriate?When the subgroup sample size is n=30 then the appropriate control chart is the Xbar and S Chart.

To understand why, please read my blog post on this topic.Now, let me comment on the last sentence of this question.Around 10 such sample were taken per day. I do not like how this part of the question is worded.

I would like to suggest that it should be worded like this. Ten subgroups were collected per day.Since there were ten Xbar values then why would we say ‘around’ 10 were collected per day? Also, samples refer to units that make up a logical subgroup. So when the question states 10 such sample were taken per day that could be interpreted to mean that each subgroup contains 10 samples.

BUT, the question begins by saying that 30 packets were taken per hour so this implies that there are 30 consecutive samples per subgroup – very confusing.So my recommendation is to please rewrite the question so that its interpretation is clear.As for question no. I would not compute control limits based on Range Values where each range value is the difference based on n=30 samples. Please refer to my blog post on Xbar Charts. In that blog post, I illustrate how that the efficiency of the Range decreases as the subgroup sample size increases.

As such, the calculation of the control limits based on the Range when n=30 is suspect.Best Regards,Andrew. X BAR AND R VALUES FOR THE 10 SAMPLES OF TEA CONTAINING 30 PACKETSX Bar: 320 310 330 360 290 280 340 320 360 300R: 12 16 14 18 22 23 10 13 27 25A packaging machine packs tea in plastic packets. To ensure consistent quantity in each packet a sample of 30 packets were taken per hour in a day and its mean and range is recorded. Around 10 such sample were taken per day. From the following data answer the following questions.Q.No 1: Comment on the type of data being collected, which control chart is appropriate for the data and why.Q.No 2: what are the values for Central Line, Upper control limit and lower control limit, also show the entire calculations for the responseAnd yes i have 10 subgroups with 30 observations.

So it means n=10 and for that constant A2= 0.308 right??Can i apply xbar r chart to this???? The question implies that 30 samples where taken each hour for a total of 10 hours (where 10 hours = 1 day). If so, then each hour 30 consecutive samples were collected and the total sample size across 10 hours would be 10 x 30 = 300 samples. If this is correct, then we have 30 samples per subgroup. However, the last sentence implies that the total sample size is 30 across 10 subgroups – this implies each subgroup is n=3. So, does each Xbar represent the average of n=3 or n=30 samples? Once we answer this question, then I can have a more informed opinion to the question.

X BAR AND R VALUES FOR THE 10 SAMPLES OF TEA CONTAINING 30 PACKETSX BarRJhilimil Tea company has a packaging machine which pack tea in plastic packets, to ensure consistent quantity in each packet a sample of 30 packets were taken per hour in a day and its mean and range is recorded. Around 10 such samples were taken per day from the following data answer the following questions.Q.No 1: Comment on the type of data being collected, which control chart is appropriate for the data and why.Q.No 2: what are the values for Central Line, Upper control limit and lower control limit, also show the entire calculations for the responseQ.No 3: What are your interpretations for the above samples, can we accept that the system is in control, give justification for your answer. X BAR AND R VALUES FOR THE 10 SAMPLES OF TEA CONTAINING 30 PACKETSX Bar: 320 310 330 360 290 280 340 320 360 300R: 12 16 14 18 22 23 10 13 27 25A packaging machine packs tea in plastic packets.

To ensure consistent quantity in each packet a sample of 30 packets were taken per hour in a day and its mean and range is recorded. Around 10 such sample were taken per day. From the following data answer the following questions.Q.No 1: Comment on the type of data being collected, which control chart is appropriate for the data and why.Q.No 2: what are the values for Central Line, Upper control limit and lower control limit, also show the entire calculations for the response.Q.No 3: What are your interpretations for the above samples, can we accept that the system is in control,give justification for you answer.Can you please solve this with explanation. X BAR AND R VALUES FOR THE 10 SAMPLES OF TEA CONTAINING 30 PACKETSX Bar: 320 310 330 360 290 280 340 320 360 300R: 12 16 14 18 22 23 10 13 27 25A packaging machine packs tea in plastic packets. To ensure consistent quantity in each packet a sample of 30 packets were taken per hour in a day and its mean and range is recorded. Around 10 such sample were taken per day. From the following data answer the following questions.Q.No 1: Comment on the type of data being collected, which control chart is appropriate for the data and why.Q.No 2: what are the values for Central Line, Upper control limit and lower control limit, also show the entire calculations for the responseCan you please let me know if I should employ an Xbar and R chart t- OR – Xbar and S chart.

Hello Amuthan.A2 is a function of the subgroup sample size. In your case if the subgroup sample is n = 45 and you plan to eventually reduce that sample size to n=20. I would not use an Xbar and Range chart.

Instead I would recommend the Xbar and S chart.Using the Range to estimate within subgroup variation deteriorates as n gets large (ie. N 10) so the Xbar and S chart is better suited.

For this type of control chart, the equivalent A2 estimate to compute the control limits for the Xbar Chart uses the C4 constant instead of d2 constant.Thank you for asking this question. I hope to write another article that discusses the Xbar and S Chart.Best Regards,Andrew.